2024. 10. 03
행렬(Matrix): 숫자나 문자를 일정한 순서에 의해 괄호 안에 배열(array)한 것으로 일반적으로 영문 대문자로 표기함.

영문 대문자 및 원소 표현
이런식으로 직접 표기할 수 있다.
또한 행렬은 열벡터들의 배열로 볼 수 있고, 행벡터들의 배열로도 볼 수 있다.

약간 이런 느낌이다.
예를 들어 a(1*C)는 A의 A의 1번째 열벡터라고 말함
Remark) 다음의 경우 앞으로 쓰게될 행렬의 일반적인 표기와 명칭이다.
- 행렬의 크기는 행(row)의 수와 열(column)의 수로 표기하는데 m행 n열 행렬의 경우 ‘m x n 행렬’이라고 쓰고, m by n 행렬 이라고 읽는다
- 행렬을 표기할 때 번거로움을 줄이기 위해 m x n 행렬인 A의 경우 A = {aij}mxn 이라고 표기한다.
- 행렬을 이루는 숫자나 기호를 그 행렬의 ‘원소’라고 하며, (A)ij란 행렬 A의 i번째 행의 j번째 열에 있는 원소 aij를 의미함.
- 행렬 0(mxn)은 모든 원소가 0 으로 구성되어있고, 크기가 mxn인 영행렬(null matrix)라고 한다
- 행렬 A(mxn)에 스칼라 c를 곱하면 벡터와 마찬가지로 행렬의 모든 원소에 c를 곱하는 것을 의미한다. 즉 cA={caij}mxn 이다.
- 행렬 A(men)에서 행과 열의 수가 같을 때, Amxn을 정방행렬(square matrix)이라고 한다.
행렬의 덧셈과 뺄셈: 앞에서 배운 벡터와 벡터간의 연산작용 벡터와 스칼라 간의 곱셈이 아닌 행렬과 행렬간의 연산작용으로
행렬의 덧셈과 뺄셈은 해당 원소간의 덧셈과 뺄셈으로 정의됨.

이런식으로 표기가 되며 정의 된다.
예시로 값을 대입해보면
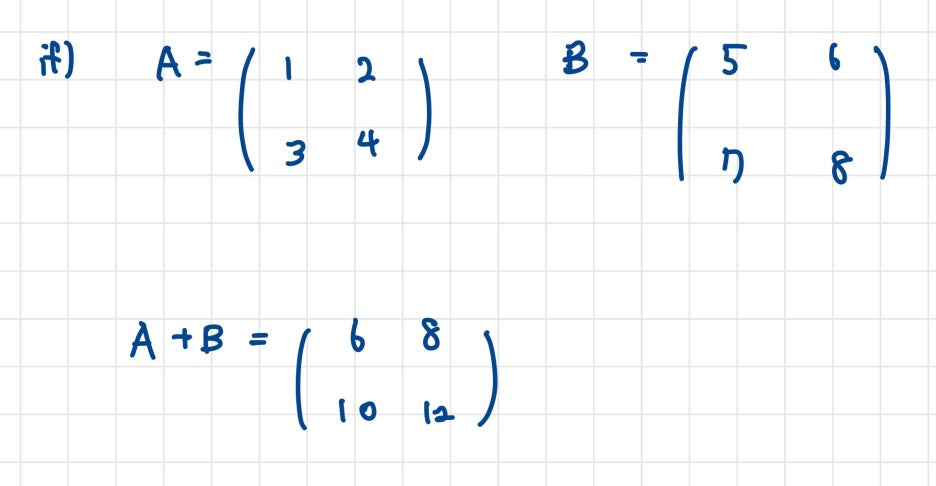
따라서 덧셈의 정의를 통해
A + A = 2A
A + A + A = 3A 이런 등식 또한 성립을 하게 되는데
증명의 경우 각 행렬에 대해 i x j인 원소 위치인 m x n행렬을 각각 더해주면 동일한 원소끼리의 덧셈이므로 2배를 해주면 되는걸
쉽게 증명 할 수 있다. (증명 생략)
행렬의 전치(Transpose)
행렬의 전치는 벡터의 전치와 같은 개념으로 이전 게시물을 봐보면 동일하다는 것을 알 수 있다.

쉽게 말하면 i행 j열에 위치한 원소값이 전치가 된다는 말은 j행 i열에 위치한 원소로 바뀐다는 말이다.
만약 i행 j열에 위치한 원소 값이 4이고 j행 i열에 위치한 원소 값이 3이라면,
이를 전치(Transpose)해 줬을때 i행 j열에 위치한 원소값이 3, j행 i열에 위치한 원소 값이 4라는 말
또한 전치행렬에 대해 다음과 같은 성질이 성립한다
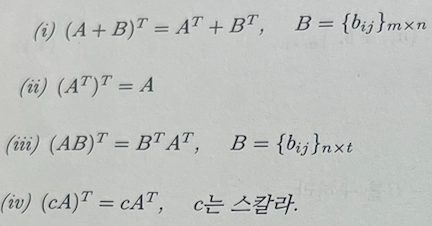
i) 의 경우 원소끼리의 위치만 바꾸고 그 원소들 끼리 더하는 거기 때문에 가볍게 증명이 가능
ii) 의 경우 원소를 한번 전치했다 다시 한번 더 전치 하는거기 때문에 i x j 위치 원소가 j x i -> i x j 로 그대로 돌아오므로 증명가능.
iii) 의경우는 행렬의 곱셈을 배운 뒤 증명 가능.
iv) 의 경우 c의 값은 스칼라 단지 상수 값이기 때문에 전치를 하더라도 변하지 않기에 증명이 되는 걸 알 수 있다.
또한 참고로 A(nxn)이 A transpose 한 행렬과 A 행렬이 같다면 A는 대칭 행렬(symmetric matrix)라고 한다.
벡터의 외적(Outer Product)
벡터의 외적에 앞서 벡터의 내적은 스칼라인 반면에 벡터의 외적은 n x n인 행렬로 계산이 된다.

벡터와 행렬의 곱셈
벡터와 벡터간의 곱셈이 내적과 외적으로 정의된 것 처럼 벡터와 행렬간의 곱셈도 같은 방식으로 정의될 수 있다.
ex) A가 m x n 인 행렬이고, x가 n x 1 벡터를 나타낸다고 하면, 행렬과 벡터의 곱셈의 결과는 m x 1 벡터인 c로 정의된다.
이때 보면 알겠지만 A와 x 가 곱해지는 경우 A의 열의 갯수, x의 행 갯수가 일치해야 한다.

원소적으로 접근해 봤을 때 A의 한 행과 x의 1열의 곱을 해보면

이런 결과를 가져올 수 있다. (글씨 이해 부탁합니다)이를 일반화 해보면
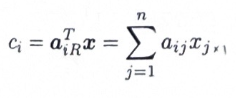
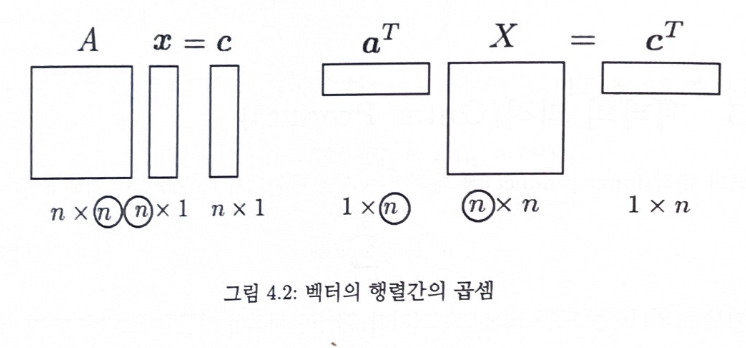
이런 느낌으로 이해. 이때 at의 경우 행벡터 이고 위에 식에 행과 열을 곱해주는 것을 일반화 한 것이다.
반면 만약 at(transpose)가 n x 1인 행벡터 이고 X가 n x n행렬이면 이 곱셈인 atX 곱셈은 1 x n인 행벡터가 된다

이를 원소를 대입해서 해본다면 쉽게 이해 할 수 있다.
행렬과 행렬의 곱셈
행렬과 행렬사이에 곱셈은 앞에 위치한 행렬의 ‘열의 수(number of columns)’와 뒤에 위치한 행렬의 ‘행의 수(number of rows)’가
일치하는 경우에만 존재하며, 곱셈 AB의 경우, 앞 행렬의 행 벡터와 뒷 행렬의 열 벡터를 내적한 행렬로 이루어 진다.

앞에 내용들과 비슷한 맥락이라 이해가 쏙쏙 된다.
행렬과 행렬의 곱셈 성질을 이용하여
A가 정방행렬 인 경우 AA = A^2 , AAA = A^3라고 표기할 수 있다.
예시를 하나 풀어 보자면

A의 경우 2 x 3행렬, B의 경우 2 x 2 행렬이기에 AB or BA를 구하기 앞서 AB행렬은 A열 값과 B행 값의 크기가 다르기 때문에
행렬과 행렬의 곱셈을 진행할 수 없고, BA행렬의 경우에는 각각 2라는 값으로 일치하기 떄문에 곱셈을 진행할 수 있다.
iii) 행렬과 행렬의 곱셈을 배웠으니 전치행렬에 관련 성질 3번째를 증명해보면

(쉽지 않았네요,,, 적고 머리로 이해하는데 30분걸린듯,,)
'선형대수' 카테고리의 다른 글
| 스칼라, 벡터, 행렬 (1) | 2024.10.10 |
|---|---|
| 선형대수에 앞선 간단한 미분 (3) | 2024.10.10 |
