2024. 10. 02
유클리드 공간(Euclidean Space): 집합 R을 모든 실수의 집합이라고 할 때, 기하학적으로 유클리드 1차공간(Euclidean 1-space)이라고 한다. 친숙한 xy좌표공간은 유클리드 2차공간이라 하며 R^2라고 표기한다.
또한 3차원인 경우 R^3인 유클리드 3차공간이며, 이러한 유클리드 공간 위의 모든점은 원점으로 부터의 거리와 각도로 표현가능하게된다.
n차원 유클리드공간은 n개의 좌표축으로 이루어짐. (선형대수에서 배우는 벡터와 스칼라는 이런 유클리드 공간에서 정의됨.)
스칼라와 벡터(Scalar and Vector): 물리학이나 수학에서 스칼라(scalar)는 크기를 나타내는 값을 의미.
ex) 무게나, 길이를 나타내는 값은 다 스칼라이다.
한편, 벡터(vector)는 두 개 이상의 스칼라를 묶어서 수평하게(행으로) 혹은 수직하게(열로) 나열해 놓은 것으로서,
크기와 방향을 모두 포함하고 있다.

벡터는 괄호안에 몇 개의 원소가 존재하는지에 따라서 그 크기가 결정되는데, 만약 원소가 3개면 R^3공간에 속하는 3X1 벡터 이고,
2개면? R^2에 속한 2X1벡터 라고 할 수 있다. 위에 그려진 원소값의 경우 3X1 벡터이며, R^공간에 속함.
데카르트 좌표계(Cartesian Coordinate): 벡터 표현하는 방법을 좌표계의 점으로 표기하는 방법.

스칼라와 벡터의 크기
스칼라의 크기는 절대값( |•| )으로 나타내지만, 벡터의 크기는 데카르트 좌표계에서 정의되는 원점으로 부터의 거리로서 ||a||라고 표기한다.
a가 유클리드 3차원 공간에 속해있는 경우, 벡터 a의 크기는 피타고라스 정리에 의해 ||a|| = (a1^2+ a2^2+ a3^2)^0.5라고 계산되고,
이를 벡터 a의 노옴(norm)이라고 한다. (맥북로 식 쓰기 어렵네요)

formula editor를 써보면 약간 이런느낌인 듯 싶습니다!
벡터의 연산작용: 벡터의 연산은 같은 차원이아닌 다른 차원간의 덧셈과 뺄셈은 불가능하고, 결국 스칼라와 스칼라 사이의 연산작용이 아닌,
스칼라와 벡터의 곱셈은 스칼라의 값을 그 벡터의 구성요소에 각각 곱해주는 것으로 정의된다.

약간 이런식으로 스칼라 a와 벡터 x간의 곱셈이 정의된다.
이처럼 벡터와 스칼라의 곱셈은 벡터의 길이에 영향을 주게되고 벡터 x의 길이(norm)을 a배 하는 역할을 하게 되며,
a가 음수인 경우에는 x의 방향이 반대로 바뀌게 한다.
추가적으로 벡터의 덧셈(혹은 뺄셈)은 같은 차원의 공간에서 정의된 벡터 간에서만 허용이 되는데,
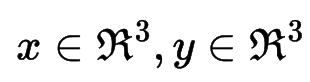
다음과 같은 동일한 차원의 공간에서만 덧셈/뺄셈이 가능하며

이런식으로 정의된다.
Remark(=참고) 영벡터는 벡터의 모든 원소가 0 으로 이루어진 벡터이다
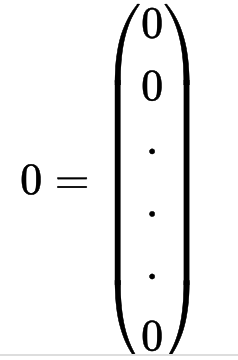
이런 식으로 쓸 수 있다.

벡터 에 대해 다음이 성립한다
- x + y = y + x
- (x + y) + z = x + (y + z)
- x + 0 = x
- x + (-x) = 0
- c(x + y) = cx + cy (c는 스칼라)
- (c+d)x = cx + dy (c,d는 스칼라)
- 1x = x

이런식으로 벡터를 여러개 만든 다음 7개의 식에 각각 대입해보면 어렵지 않게 증명 가능하다.
벡터의 내적(Inner Product):
벡터의 내적에 앞서 우선 벡터의 전치란 벡터를 구성하는 원소의 행을 열로, 열을 행으로 바꿈으로써 열벡터를 행벡터로,
혹은 행벡터를 열벡터로 표현하는 과정을 말하며 윗첨자 T를 첨부해 표시함. a의 전치는

이런식으로 표기해 주면 된다.
예시)

definition: 벡터의 내적(Inner product)이 정의되기 위해서는 곱해지는 두 개의 벡터가 모두 같은 차원으로 속해야 하며,
두 벡터 x와 y의 내적은

예시의 경우 위의 식에 숫자만 대입하면 되기때문에 생략.
벡터 x와 벡터 y가 n차원 유클리드 공간에서 정의될때 두 벡터 사잇각에 대하여 내적 값은 아래와 같은 성질을 만족함

(어렵네요 일일이 쓰기.. 기호쓰기좋은 맥북 앱 있으면 추천 부탁합니다)
내적의 증명은 이런식으로 진행하면 좋은거 같아요.

직교벡터 (Orthogonal Vectors): 직교벡터란 내적의 개념을 잘 알았다면 금방 적용 하기 쉬운데
두 벡터 간의 사잇각이 직각을 이룬다면 두 벡터는 서로 직교한다 말하며, 두 벡터간의 내적의 값은 0이된다
그 이유로는 사잇각 세타에 대하여 cos(90)의 값이기 때문에 0을 이루므로 벡터의 크기값과 관계없이 항상 0이 된다
영벡터가 아닌 두 벡터가 있을 때 벡터의 내적이 0이면 두벡터는 서로 직교이므로 역도 성립한다.
추가적으로 직교하는 두 벡터의 길이가 각각 1일 경우, 이 벡터를 ‘직교정규벡터’라고 말함.
다음의 경우 직교 정규 벡터이다.

이때 벡터의 크기(norm) 값은 1이고, 서로 다른 벡터간의 내적이 0인경우를 말함.
이를 활용해 항상 길이가 1인 단위벡터로 만들어 정규화 벡터로 사용도 가능하다!
코쉬-쉬바르츠 (Causchy - Schwartz) 부등식
실수 xi와 yi (i= 1, 2, …, n)에 대하여 아래 부등식이 항상 만족하며 이를 ‘코쉬- 슈바르츠 부등식’ 이라고 함.

이를 증명하기 위한 여러가지 방법이 있으나 내적의 성질을 사용하면 쉽게 증명이 가능하다.
마지막으로 지피티한테 받은 사진 투척

'선형대수' 카테고리의 다른 글
| 행렬의 기본 개념 (4) | 2024.10.10 |
|---|---|
| 선형대수에 앞선 간단한 미분 (3) | 2024.10.10 |
